Some background on DMFT and the Mott MIT
This work is devoted towards obtaining Hamiltonian-based insight into the dynamical mean-field theory (DMFT) treatment for the half-filled Hubbard model on the Bethe lattice in infinite dimensions. Our work offers an effective auxiliary model Hamiltonian that incorporates the effects of a local interacting self-energy (as obtained from the self-consistent approach of DMFT), and provides insight on the associated Mott metal-insulator transition (MIT). We recall that the conduction bath (of the effective impurity model within DMFT) becomes correlated under the requirement of self-consistency. The numerical implementation of this process precludes a deeper understanding of the precise nature of the correlations present in the conduction bath, and its implications for the electron dynamics of the associated bulk lattice (Hubbard) model.
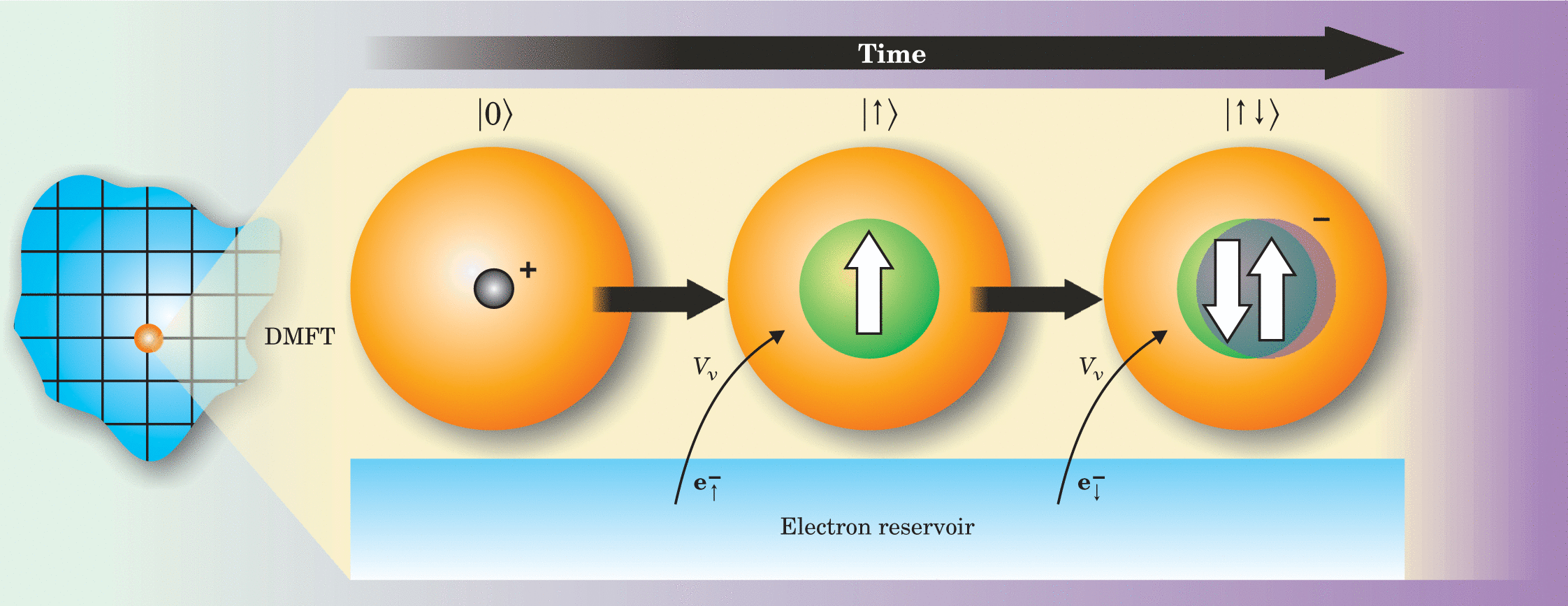“Dynamical mean-field theory (DMFT) of correlated-electron solids replaces the full lattice of atoms and electrons with a single impurity atom imagined to exist in a bath of electrons. The approximation captures the dynamics of electrons on a central atom (in orange) as it fluctuates among different atomic configurations, shown here as snapshots in time.” [Source]
Questions addressed by us in the present work
This leads to the following questions that we address in our work:
- What are the quantum fluctuations that destroy the metal at \(T=0\) and lead to the insulating phase?
- Can we obtain a universal theory for the competing tendencies that give rise to these quantum fluctuations?
- What leads to the coexistence of metallic and insulating phases within DMFT at \(T=0\), as indicated by the fact that the insulating solution is already present within the many-body spectrum of the metallic phase prior to the transition?
- Is it possible to obtain a low-energy theory for the local gapless excitations precisely at the MIT, where the metal is on the brink of destruction?
Main results: An extended Anderson impurity model and its QCP
In order to model the interactions within the bath, we adopt an extended single impurity Anderson model (e-SIAM) as the effective auxiliary model for the Mott MIT. In addition to the usual impurity on-site repulsion U and the single-particle hybridisation V, we introduce
- an additional on-site correlation (\(U_b\)) on the bath site with which the impurity couples, and
- an antiferromagnetic Kondo coupling (\(J\)) between the impurity and the conduction bath.
These additions are then justified via a \(T=0\) renormalisation group (RG) analysis of the e-SIAM that reveals a quantum phase transition (QPT) at a critical value of the ratio (\(-U_b/J\)). The transition involves a change in the ground-state from a (Kondo) spin singlet to an unscreened local moment, indicating a Mott MIT in the bulk model associated with the chosen auxiliary model similar to DMFT.
We have extended the standard Anderson impurity model by incorporating an explicit Kondo coupling \(J\) and a local correlation \(U_b\) on the bath site coupled to the impurity. Such a model shows a local metal-insulator transition.
Main results: Preformed gap = Excited state QPT
We use the fixed-point Hamiltonians obtained from the RG procedure to calculate quantifiers of the transition, e.g., various many-body correlation functions as well as measures of many-particle entanglement. These measures reveal that the transition occurs through a breakdown of the Kondo screening effect, owing to enhanced local pairing fluctuations in the bath proximate to the QPT. In the immediate neighbourhood of the transition, these pairing fluctuations also lead to the appearance of long-ranged correlations between the impurity and the conduction bath degrees of freedom, signalling critical behaviour. Remarkably, we find that the impurity QPT from metal to insulator is preceded by an excited state quantum phase transition (ESQPT): this involves the appearance of the local moment states in the many-body spectrum as excited states. This mechanism leads to a preformed (optical) gap in the impurity spectral function, as well as the coexistence region, in the phase diagram of the e-SIAM. This is consistent with the well-known phenomenology of DMFT.
Main results: Enhanced pairing fluctuations and non-Fermi liquid excitations at the Mott MIT
Further, the e-SIAM provides a minimal and universal local theory for describing Mott metal-insulator transition that arise from strong local correlations, and involves a competition between Kondo screening and its frustration from a locally correlated bath. The minimal model also offers detailed insights on the nature of the gapless excitations present at transition. We find that gapless non-Fermi liquid excitations arise from the ground state degeneracy at the transition, involving an orthogonality catastrophe and the vanishing of the quasiparticle residue of the local Fermi liquid. The non-Fermi liquid is characterised by anomalous power-law behaviour in the self-energy and various two-particle correlations, as well as a fractional entanglement entropy and magnetisation arising from a scattering phase shift of π/2.
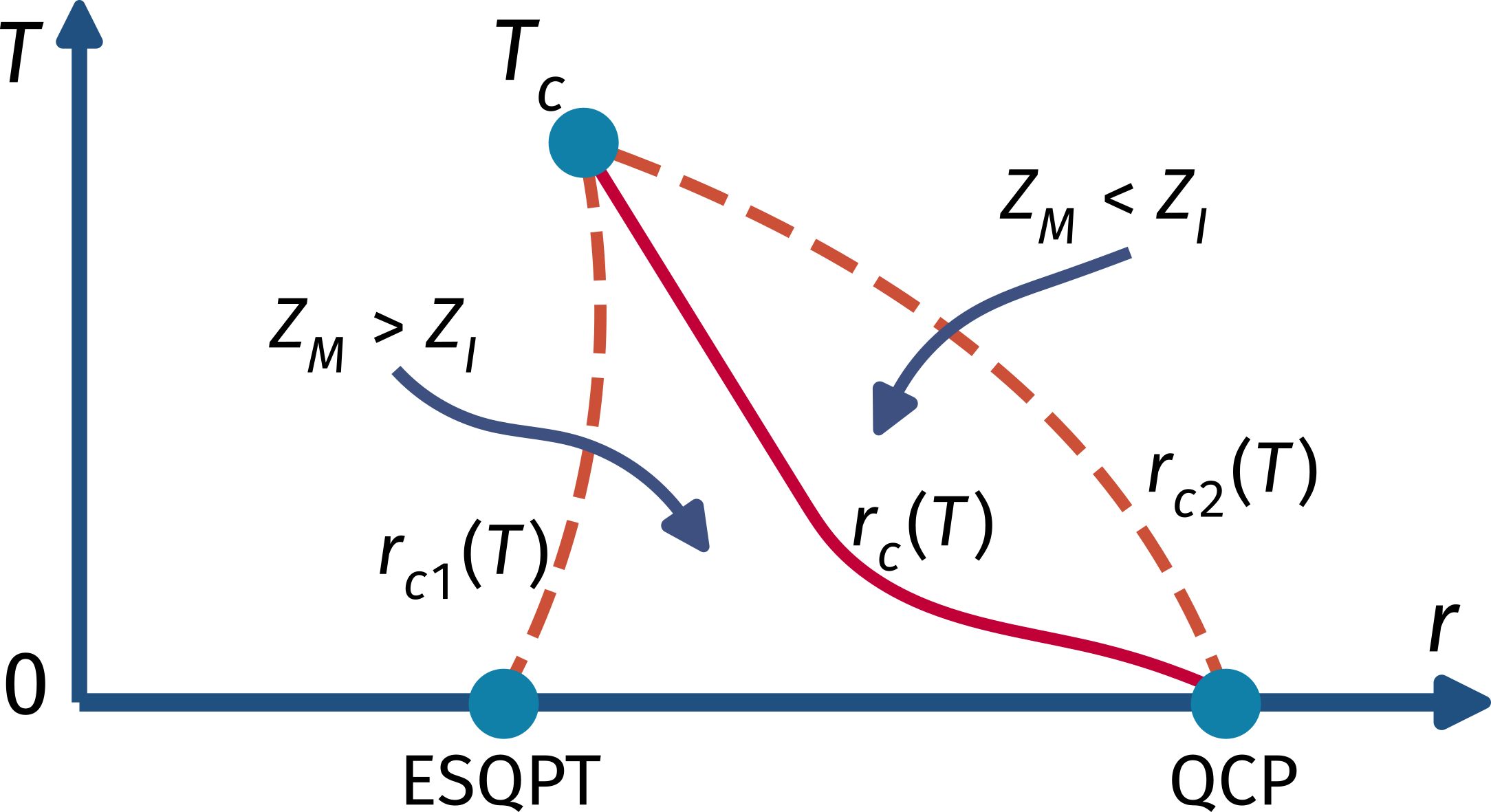Qualitative structure of the finite temperature coexistence region of the \(J - U_b\) model. The dotted lines on the left and the right represent the spinodals where the insulating and metallic solutions become unstable, respectively. The solid red line represents the first-order line where the free energies and the partition functions of the two solutions become equal.
Conclusions and outlook
Thus, our work offers a host of new results on multiple aspects of the auxiliary model approach to the Mott MIT. In general, the interplay of multiple correlations in the e-SIAM localisation from repulsion on the impurity site (\(U\)), delocalisation from spin and charge fluctuations (\(J\) and \(V\)), and pairing from local attractive correlations in the bath (\(U_b\)) - makes this a strong candidate for describing the emergence of a variety of novel phases of correlated quantum matter. Likely future investigations include, for instance, the effects of hole doping on the nature of the local quantum criticality observed by us, and especially whether critical pairing fluctuations can condense into a superconducting state of matter.