Abhirup

Graduate student in physics, IISER Kolkata

A bit of background

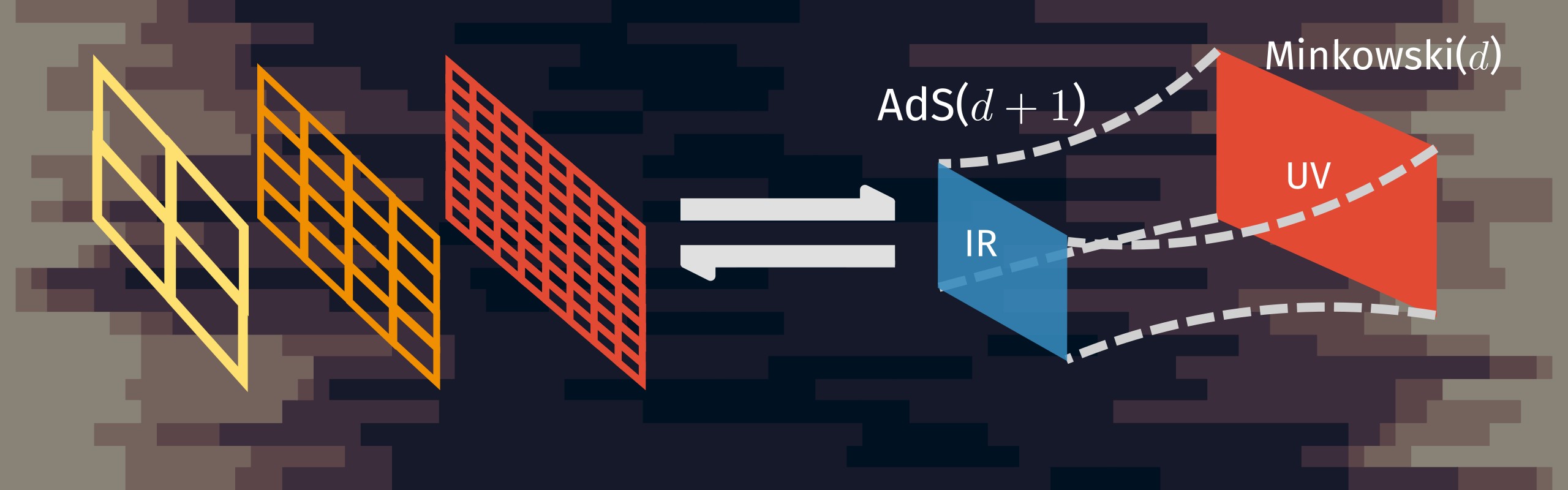
In the last few decades, quantum entanglement has become very important for studying the nature of quantum condensed matter systems. For instance, gapped interacting many-body systems typically display an area-law scaling of the subsystem entanglement entropy with subsystem size, while quantum critical systems are expected to display a volume law scaling of the same. Further, a subdominant topological term in the entanglement entropy quantifies the long-ranged nature of correlations in topologically ordered insulating states of matter. Much less is known on the entanglement features of gapless metallic systems. Further, the holographic principle posits that the renormalisation group evolution of the many-particle entanglement of an interacting quantum field theory can be visualised as the emergence of an emergent spatial dimension.

Questions addressed

The present work is thus devoted towards addressing the following questions:

  • Can a first principles calculation of entanglement renormalisation in a relatively simple system demonstrate the holographic emergence of a spatial geometry?
  • How do the field theoretic parameters (e.g., the RG beta function) relate to the geometry quantifiers (e.g., distances and curvature) in this emergence dimension?
  • Spectral flow operations on metallic systems lead to a flux-dependent piece in the entanglement entropy. Is this term topological in nature?
  • If so, is there a correspondence between the topological terms in metallic systems and those obtained in the above-mentioned insulating systems?

Main results of our work

Towards achieving these goals, we study a model of two-dimensional massive non-interacting Dirac fermions placed on a torus, and apply scaling transformations on the associated Hilbert space. The resultant renormalisation of multipartite measures of entanglement exhibits a hierarchy that exists across energy scales as well as across the number of parties. As our demonstration constitutes an exact holographic mapping, we argue that the scaling of the multipartite entanglement leads to the emergence of an additional spatial dimension. Geometric measures defined in this emergent space, such as distances and curvature, can be related to the RG beta function of the coupling g responsible for the spectral mass gap. Depending on the anomalous dimension of g, three classes of spaces (bounded, unbounded and flat) are generated from the RG: changing between classes involves a topological transition.

In order to study the boundary condition sensitivity of the multipartite entanglement, we thread an Aharonov-Bohm flux through the torus. In the presence of the flux, the entanglement gains a geometry-independent piece that is shown to be topological, and can be related to the Luttinger volume of the system of electrons. In the presence of a strong transverse magnetic field, the system attains an integer quantum Hall insulating ground state, and Luttinger’s theorem does not hold. We show instead that the entanglement contains a term that can be related to the Chern numbers of the integer quantum Hall states. This yields a relation between the topological invariants of the metallic and the integer quantum Hall systems.

Thus, our work offers an ab initio demonstration of the holographic principle in a prototypical condensed matter system, and sheds new light on geometrical and topological aspects of entanglement in metals.

You May Also Enjoy